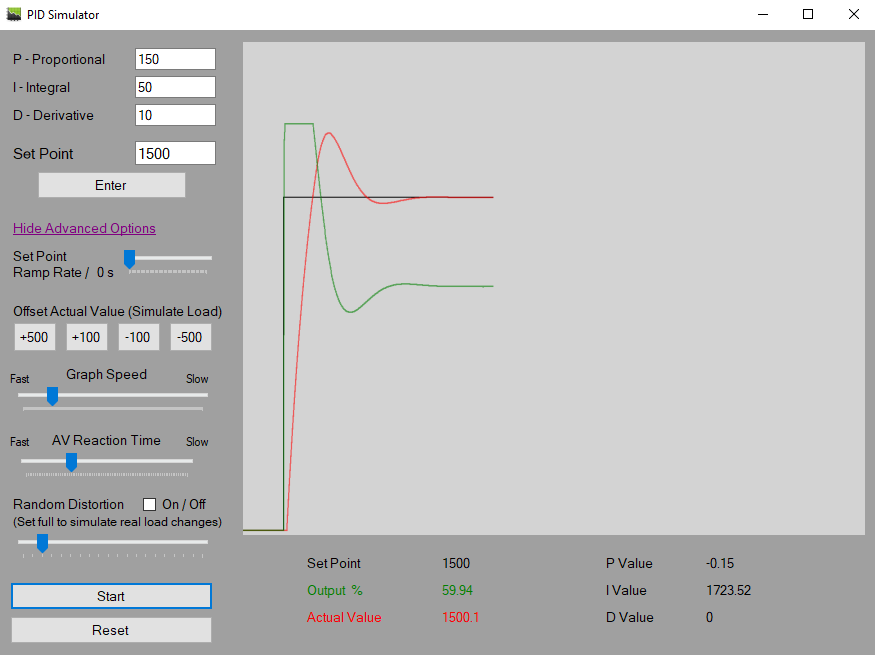
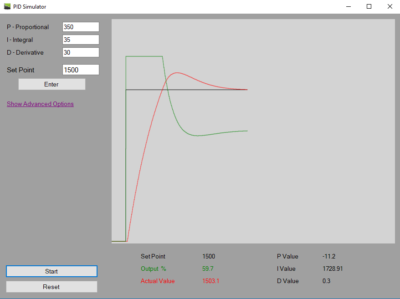
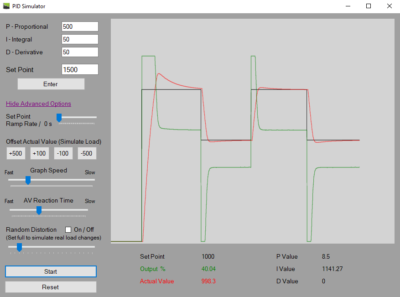
A PID (Proportional Integral Derivative) controller works by controlling an output to bring a process value to a desired set point.
See post “WHAT IS A PID CONTROLLER?” for a basic example of a PID controller. And also the PID Simulator page to use a live PID Simulator!
Before we dive into the PID controller, there is a few terms that need defined:
PID Controller Terms:
Set Point
The set point is normally a user entered value, in cruise control it would be the set speed, or for a heating system, it would be the set temperature.
Process Value
The process value is the value that is being controlled. For cruise control this would be the actual vehicle speed, or in a heating system, this would be the current temperature of the system.
Output
The output is the controlled value of a PID controller. In cruise control, the output would be the throttle valve, in a heating system, the output might be a 3 way valve in a heating loop, or the amount of fuel applied to a boiler.
Error
The error value is the value used by the PID controller to determine the how to manipulate the output to bring the process value to the set point.
Error = Setpoint – Process Value
PID Controller Explained!
The basic explanation of a PID controller. The PID controller is continuously monitoring the error value, and using this value, calculates the proportional, the integral and the derivative values. The controller then adds these three values together to create the output.
Below we will dive into the proportional, integral and derivative as three separate equations, then add them together to create the output, but first, we need to talk about the user input values in the PID controller… the gain settings (P-Gain, I-Gain and D-Gain).
Gain
Gain is the term used for “multiplication factor”. By adjusting the gain settings (or multiplication factor) of the proportional, the integral and the derivative, the user can control how much effect the PID controller has on the output, and how the controller will react to different changes in the process value.
P or Proportional
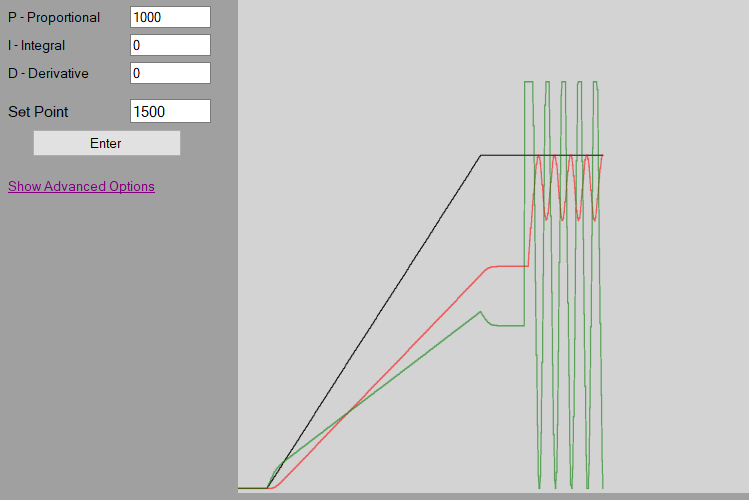
The Proportional is calculated by multiplying the P-Gain by the error. The purpose of the proportional, is to have a large immediate reaction on the output to bring the process value close to the set point. As the error becomes less, the influence of the proportional value on the output becomes less.
The Proportional math looks like this:
P = Proportional | kP = Proportional Gain | SP = Set point | PV = Process Value | Err = Error
Err = SP – PV
P = kP x Err
I or Integral
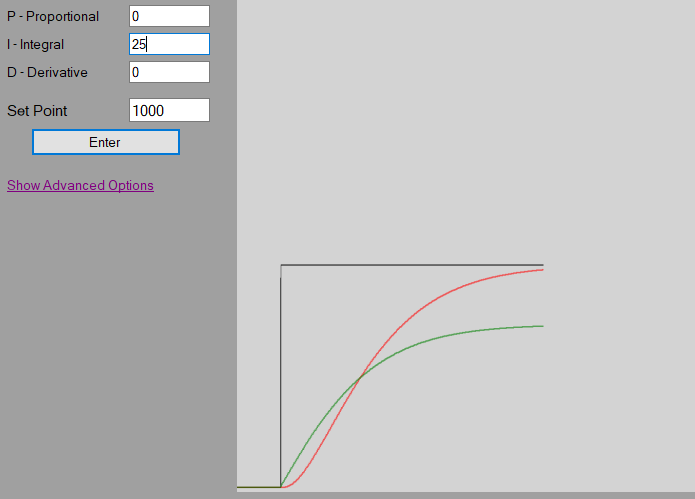
The Integral is calculated by multiplying the I-Gain, by the error, then multiplying this by the cycle time of the controller (how often the controller performs the PID calculation) and continuously accumulating this value as the “total integral”.
Explained a little further, every time the controller performs the PID calculation (example of a cycle time is every 100 ms), the new calculated integral value, is added to the integral total. The integral will normally not have as much immediate influence on the output as the proportional, but because the integral is continuously accumulating overtime, the longer it takes for the process value to reach the set point, the more effect the integral will have on the output.
And the Integral math:
I = Integral | kI = Integral Gain | dt = cycle time of the controller | It = Integral Total
I = kI x Err x dt
It = It + I
D or Derivative
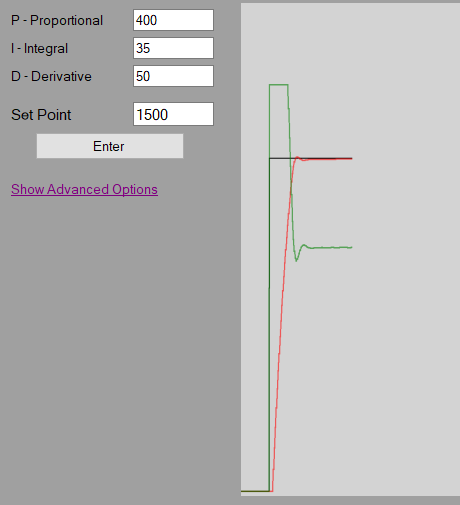
The derivative is calculated by multiplying the D-Gain by the ramp rate of the process value. The purpose of the derivative is to “predict” where the process value is going, and bias the output in the opposite direction of the proportional and integral, to hopefully prevent the controller from over-shooting the set point if the ramp rate is to fast.
Explained a bit simpler, if the process value is approaching the set point to fast, the derivative will limit the output to prevent the process value from overshooting the set point.
The Derivative Math:
D = Derivative | kD = Derivative Gain | dt = cycle time of the controller | pErr = Previous Error
D = kD x (Err – pErr) / dt
Output
The PID controller output is calculated by simply adding the Proportional, the Integral and the Derivative. Depending on the gain setting of these three values, will determine how much effect they will have on the output.
PID Controller Output Math:
Output = P + It + D
All together a PID control loop looks like this;
Err = Sp – PV
P = kP x Err
It = It + (Err x kI x dt)
D = kD x (pErr – Err) / dt
pErr = Err
Output = P + It + D
Wait dt (100 ms), and perform loop again.
Tuning a PID controller
Check out this post to learn how to tune a PID controller and how to set one up from scratch.